Relevanz und regulatorische Anforderungen
Bei variablen Produkten handelt es sich um Produkte, deren Cashflowstruktur nicht deterministisch abgeleitet werden kann, da keine vertragliche Laufzeit und/oder Zinsbindung vereinbart wurde. In der Praxis ist es mittlerweile üblich, hierfür mathematische Modelle heranzuziehen.
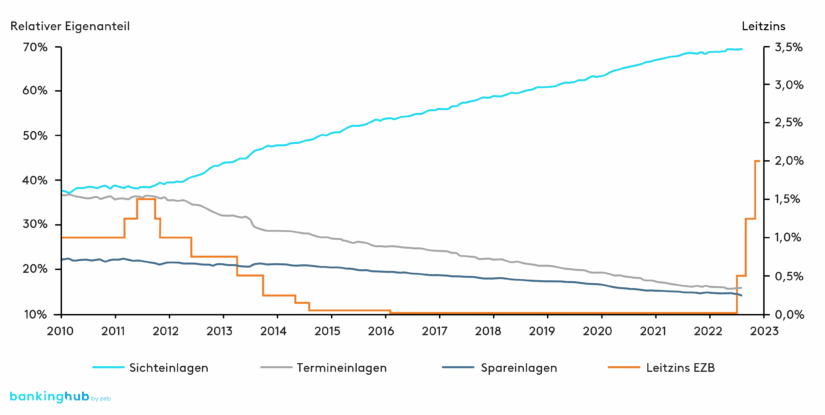
Die Ableitung und Verwendung möglichst passgenauer Cashflowannahmen ist wesentlich für eine optimierte Gesamtbanksteuerung. Die gestiegene Bedeutung von variablen Produkten mit stochastischem Cashflowprofil lässt sich zum einen durch neue oder weiterentwickelte aufsichtsrechtliche Anforderungen (z. B. EBA-IRRBB-Leitlinien[1], EZB-ILAAP-Leitfaden[2]) erklären, zum anderen aber auch durch den kontinuierlichen und signifikanten Volumenanstieg von Sichteinlagen als typisches variables Produkt in den vergangenen zehn Jahren (siehe Abbildung 1[3]).
Institute sind gemäß den Anforderungen der MaRisk zu Liquiditätsrisiken[4] (BTR 3) dazu angehalten, Liquiditätsübersichten durch die Gegenüberstellung von Mittelzu- und -abflüssen für den kurz-, mittel- und langfristigen Horizont zu erstellen. Hierbei sind sowohl das normale als auch das angespannte Marktumfeld zu berücksichtigen. Eine Modellierung von Cashflows wird damit implizit vorgegeben.
Gemäß Grundsatz 3, Artikel 43 des EZB-ILAAP-Leitfadens sind unter der ökonomischen Perspektive interne Verfahren und Methoden zu entwickeln, um erwartete und unerwartete Liquiditätsabflüsse zu identifizieren, zu quantifizieren sowie die Ergebnisse in die Festlegung des internen Liquiditätspuffers einzubeziehen. Nach Artikel 47 sind die getroffenen Ablaufannahmen aus der ökonomischen Perspektive auch in der normativen Sicht zu berücksichtigen, beispielsweise bei der Berechnung der Forward-LCR, um Konsistenz zu gewährleisten. Des Weiteren sind sie auch für Stresstestberechnungen heranzuziehen und entsprechend zu variieren.
In Bezug auf die Wahl der Methode zur Risikoquantifizierung von Liquiditätscashflows werden weder in der MaRisk noch im ILAAP-Leitfaden explizite Vorgaben gemacht. Der ILAAP-Leitfaden definiert jedoch, dass die gewählten Verfahren und Annahmen „robust, hinreichend stabil, risikosensitiv und konservativ genug sein [sollten], um selten auftretende Liquiditätsabflüsse zu quantifizieren“ (Artikel 72). Dabei besteht zusätzlich der Anspruch, dass diese Methoden vollständig verstanden werden und für die Situation und das Risikoprofil des Instituts angemessen sind (Artikel 75).
Durch die beschriebenen Marktentwicklungen und regulatorischen Anforderungen wird es immer wichtiger, dass Institute den Ablauf ihrer Bestände zuverlässig und akkurat ermitteln. Qualitative Schätzungen der Cashflowablaufprognosen aus Erfahrungswerten und Expertenwissen, die in der Vergangenheit und auch durchaus heute noch durchgeführt werden, gelten als ungenau sowie nicht reproduzierbar. Gemäß zeb-Erfahrungen aus Projekten und Prüfungsfeststellungen sind diese nicht angemessen. Es werden fundierte, quantitative Modelle seitens der Aufsicht erwartet.
Vergleich der Ansätze zur Modellierung von Liquiditätscashflows
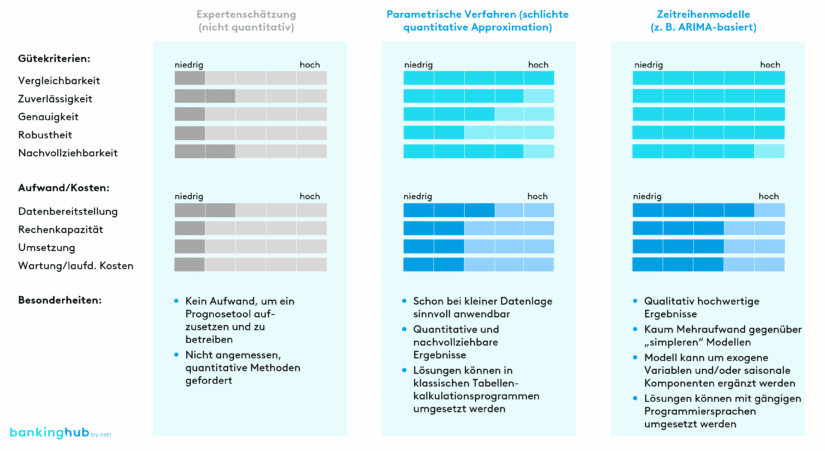
Im Folgenden werden unterschiedliche quantitative Ansätze und Methoden zur Ablaufmodellierung vorgestellt sowie ihre jeweiligen Vor- und Nachteile diskutiert. Es gibt vielfältige weitere Verfahren, die in der Modellierung einsetzbar sind (z. B. Monte-Carlo-Simulationen), auf welche jedoch in diesem Artikel nicht eingegangen wird. Die im Weiteren behandelten Methoden sind nach unserer Einschätzung in Abwägung der Kosten-Nutzen-Relation den anderen Verfahrensweisen überlegen.
Parametrische Verfahren zur Liquiditätsmodellierung
Im Kontext der quantitativen Modellierung von zukünftigen Liquiditätscashflows sind besonders parametrische Verfahren weit verbreitet. Bei diesen wird eine einheitliche Verteilung für die Cashflowveränderung zwischen zwei Zeitpunkten unterstellt und eine Approximation auf Basis historischer Daten durchgeführt. Typische Verteilungen, die hier angewandt werden, sind z. B. eine Standardnormalverteilung oder eine Log-Normalverteilung.
Da eine zeitlich konstante Verteilungsannahme vorausgesetzt wird, werden durch parametrische Verfahren Trends und saisonale Verlaufskomponenten im Ergebnis nicht berücksichtigt. Bei Bedarf können diese jedoch auch mit einem Regressionsmodell (z. B. linear, exponentiell, Sinus/Cosinus) kombiniert werden.
Trotz der undifferenzierten Approximation aller Liquiditätscashflows, z. B. durch eine Standardnormalverteilung, ist diese Methode aus unserer Sicht eine deutliche Verbesserung und sinnvolle Erweiterung zu einer rein qualitativen Schätzung, da die quantitativen Ergebnisse reproduzierbar und nachvollziehbar sind. Des Weiteren sind parametrische Verfahren durch ihre geringe Komplexität relativ ressourcenschonend und liefern schon auf Basis einer spärlichen Datenlage zuverlässige Ergebnisse. So kann das Verfahren mit wenig Aufwand aufgesetzt und betrieben werden.
Fortgeschrittene Zeitreihenmodelle (z. B. ARIMA-basiert)
Für eine noch genauere Modellierung der Liquiditätscashflows gibt es komplexere Methoden mit mehr Parametrisierungsfreiheiten. Dafür werden jedoch hochqualitative Daten auf feingranularer Ebene benötigt, um einen echten Vorteil im Vergleich mit den einfachen parametrischen Verfahren realisieren zu können. Außerdem ist gemäß dem Proportionalitätsprinzip abzuwägen, ob der Mehraufwand den zusätzlichen Nutzen rechtfertigt.
Sind diese Voraussetzungen jedoch erfüllt, sollte der Einsatz von fortgeschrittenen Zeitreihenmodellen durchaus in Erwägung gezogen werden. Insbesondere ARIMA-basierte Verfahren (Autoregressive Integrated Moving Average) gewinnen im Kontext der Modellierung von Liquiditätscashflows immer mehr an Relevanz und Beachtung. Dabei werden Zeitreihen unter der Annahme prognostiziert, dass jeder Wert zu einer gewissen Zeit t eine Abhängigkeit von den Werten der Zeitreihe vor t aufweist. So kann das Modell mithilfe historischer Zeitreihen approximiert und basierend darauf fortgeschrieben (prognostiziert) werden.
Es gibt zahlreiche Erweiterungen zum ARIMA-Modell. Eines davon ist das ARIMAX-Modell, in dem exogene Variablen ergänzt werden, um einen externen Trend zu parametrisieren. Zwar werden auch durch das ARIMA-Modell Trends abgebildet, jedoch nur solche, die auch in der historischen Zeitreihe intrinsisch vorhanden sind. Wie oben bereits erwähnt, sind es jedoch externe Faktoren, die das Volumen an Sichteinlagen treiben (z. B. Zinsanstieg, Inflation). Da äußere Einflüsse die Rahmenbedingungen über den Zeitverlauf verändern, können solche Trends auch nur über exogene Variablen dargestellt werden.
Darüber hinaus gibt es das SARIMA-Modell, in welchem ein zusätzlicher saisonaler Verlauf der Zeitreihe approximiert wird. Sichteinlagen haben normalerweise periodische Verläufe mit einer monatlichen Frequenz, die durch das SARIMA-Modell hervorragend abgebildet werden können. Im erweiterten SARIMAX-Modell werden sowohl exogene Trends als auch saisonale Verläufe berücksichtigt.
Während die Modellparameter durch Kleinste-Quadrate- und Maximum-Likelihood-Methoden objektiv geschätzt werden können, ist für eine zuverlässige Prognose der Zeitreihe die richtige Auswahl der Spezifikationsparameter von hoher Bedeutung und stellt bei der Modellierung die größte Herausforderung dar. Auch die Entscheidung, ob ein ARIMA-, ARIMAX-, SARIMA- oder SARIMAX-Modell zu verwenden ist, ist nicht immer trivial. Das SARIMAX-Modell bietet nicht zwingend eine zuverlässigere Prognose als das ARIMA-Modell, und es bedarf einer intensiven Abstimmung im Hinblick auf die vorhandenen Daten.
Es besteht die Möglichkeit, für verschiedene Spezifikationsparameter einen Best-Fit-Vergleich mit den historischen Daten durchzuführen und so die statistisch beste Auswahl für die vorliegenden Daten weitgehend automatisiert und mit wenig Aufwand zu ermitteln. Dies ermöglicht es, bei diesem Ansatz mit sehr wenig subjektiv getroffenen Annahmen zu arbeiten.
Der Vergleich mit den einfachen parametrischen Verfahren zeigt, dass mit den ARIMA-basierten Methoden signifikant genauere Ergebnisse in der Prognose erzielt werden können. Insbesondere, wenn Datenbestände über einen langen Zeitraum in kurzen Abständen (am besten täglich) vorhanden sind, kommen die Vorteile zum Tragen.
Künstliche Intelligenz (kurzer Ausblick)
Eine weitere Methode, die für die Prognose der Liquiditätscashflows denkbar wäre, ist der Forecast anhand eines Modells, das durch maschinelles Lernen generiert wird. Künstliche Intelligenz (KI) ist derzeit ein sich rasant entwickelndes Themengebiet, und die Anwendung wird in den verschiedensten Bereichen erprobt und geprüft (vgl. z. B. BankingHub-Artikel „LCR-Prognose mit KI“).
Gegenüber den zuvor beschriebenen Modellansätzen bietet diese Methode den echten Vorteil, dass das KI-Modell zusätzlich zu den historischen Bestandsdaten mit beliebigen weiteren Daten trainiert werden kann. Dadurch wird ermöglicht, dass weitere Einflussfaktoren (z. B. Kundencharakteristika oder aktuelle Marktdaten) für die Prognose der Liquiditätscashflows berücksichtigt werden.
Die größten Herausforderungen in der Implementierung bestehen zumeist in unzureichenden Datengrundlagen und einer Intransparenz der Modellergebnisse („Black-Box“-Algorithmen). Insbesondere die aufsichtsrechtliche Erwartung, dass die eingesetzten Verfahren nachvollzogen werden können, ist bei KI-Modellen somit grundsätzlich nur bedingt erfüllt, und eine Interpretation der Ergebnisse kann sich schwierig gestalten.
BankingHub-Newsletter
„(erforderlich)“ zeigt erforderliche Felder an
Herausforderungen bei der Umsetzung
Neben den beschriebenen methodischen Herausforderungen finden sich bei der Umsetzung auch viele praktische Hürden. Dies beginnt bei der benötigten Datenbasis: Oftmals sind gerade auf Produktebene keine langen Historien oder nur solche auf Monatsbasis verfügbar, sodass die Stichproben zu klein für verlässliche Prognosen sind. Liegen hingegen lange Zeitreihen vor, so sollte deren Repräsentativität kritisch hinterfragt werden.
Auch Saisonalitäten wie z. B. der Eingang eines dreizehnten Monatsgehalts sollten, sofern materiell, abgebildet werden. Weitere exogene Faktoren wie das Zinsniveau, BIP, Inflation etc. sollten abhängig von ihrer ermittelten Signifikanz berücksichtigt werden. Für die zugehörigen statistischen Tests ist wiederum eine gute Datenbasis erforderlich.
Eine Kunst besteht zudem in der richtigen Wahl der Portfolioschnitte, damit einerseits die Spezifika der verschiedenen Produkte und Kundensegmente modelliert werden. Andererseits sollte auch eine Materialitätsschwelle gewahrt bleiben, und einzelne Kunden sollten nicht das Verhalten eines Portfolios bestimmen, da dadurch die Möglichkeit einer statistischen Modellierung verloren geht. Insbesondere im Wholesale Banking sollte die Notwendigkeit geprüft werden, das Liquiditätsrisiko sehr großer Geschäfte gesondert zu modellieren.
Die Dimension des gewählten Modells sollte sich gemäß dem Proportionalitätsprinzip am Geschäftsmodell und an der Komplexität des jeweiligen Instituts orientieren. Es kann durchaus vorteilhaft sein, einem eher einfachen Ansatz gegenüber einem sehr komplexen Modell den Vorrang zu geben, wenn damit trotzdem eine gute Prognosegüte erzielt werden kann.
Sowohl betriebswirtschaftlich als auch aufsichtlich ist es notwendig, die Ergebnisse zu interpretieren, um sie sinnvoll in die Banksteuerung einbinden zu können. Hierfür ist erforderlich, dass auch neue Entwicklungen wie z. B. Zinsportale und Vergleichsplattformen, die zukünftig eine geringere Kundentreue erwarten lassen, in einem Modell adäquat berücksichtigt werden.
Um gegenläufige Steuerungsimpulse zu vermeiden, ist es ebenfalls wichtig, eine bereichsübergreifende, einheitliche Modellierung vorzunehmen. Ein Beispiel hierfür ist insbesondere die Sicherstellung der Konsistenz und Überleitbarkeit der im Risikocontrolling sowie im FTP (Funds Transfer Pricing) verwendeten Modellierungsannahmen und Cashflows.
Modellierungsansätze sind nach institutsspezifischen Begebenheiten zu evaluieren
Wir haben unterschiedliche quantitative Ansätze zur Modellierung von Liquiditätscashflows bei variablen Produkten verglichen und stellen fest, dass es keine universal optimale Lösung gibt. Hier sind der Aufwand und Nutzen der jeweiligen Ansätze für jedes Institut individuell abzuwägen.
Insbesondere die Bereitstellung von qualitativ hochwertigen Daten stellt einige Institute vor Herausforderungen. Ist eine solche Datenbasis nicht verfügbar, wird auch ein sehr fortgeschrittenes Zeitreihenmodell keine signifikant genaueren Ergebnisse liefern können, und es empfiehlt sich, einfachere parametrische Verfahren anzuwenden. Sind jedoch genauere Prognosen gewünscht, unter Berücksichtigung von nichtstationären Strukturen wie z. B. Saisonalitäten oder auch exogenen Faktoren, eignen sich bei vorhandener qualitativ hochwertiger Datenbasis fortgeschrittenere Methoden wie die ARIMA-basierten Verfahren.