Anpassungen und Weiterentwicklungen von Kreditportfoliomodellen nur bedingt umgesetzt
Die bisherigen Erfahrungen zeigen, dass in vielen Instituten die geforderten Anpassungen und Weiterentwicklungen von Kreditportfoliomodellen nur bedingt umgesetzt worden sind oder sogar noch gänzlich ausstehen, sodass diesbezüglich vielerorts ein direkter Handlungsbedarf identifiziert werden kann.
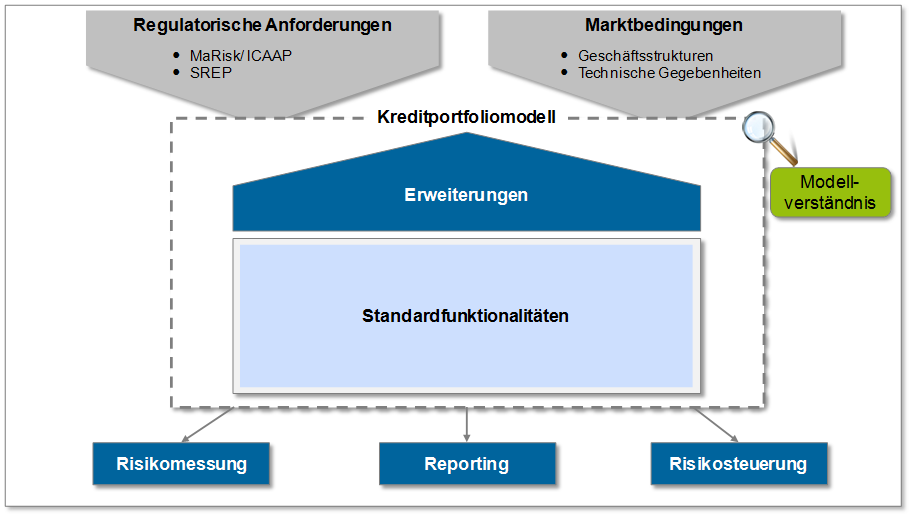
Sowohl anhand der regulatorischen als auch anhand der marktseitigen Bedingungen ergeben sich direkte Anforderungen an die Funktionalitäten (Standardfunktionalitäten und mögliche Erweiterungen) von Kreditportfoliomodellen, die die Erfüllung der wesentlichen Funktionen dieser Modelle – Risikomessung, Reporting und Risikosteuerung – ermöglichen sollen (vgl. Abbildung 1).
Funktionen und Funktionalitäten von Kreditportfoliomodellen
Der wesentliche Nutzen von Kreditportfoliomodellen liegt in ihrem Einsatz in der (Kredit-) Risikomessung begründet. Neben der Bestimmung des erwarteten Verlustes und der Verlustverteilung von Kreditportfolios und somit auch einer Einschätzung der Höhe des benötigten Eigenkapitals anhand wesentlicher Standardrisikomaße wie dem Value-at-Risk und dem Expected Shortfall, können durch adäquate Kreditportfoliomodelle Klumpenrisiken, d.h. volumensbasierte Kreditrisikokonzentrationen (zum Beispiel einzelner Branchen oder Länder), sowie hohe Einzelrisiken ermittelt und ausgegeben werden. Vor allem in letzterem Aspekt liegt der Vorteil von Kreditportfoliomodellen gegenüber der Verwendung von Standardformeln begründet, da Verlustbeiträge einzelner Kreditnehmer basierend auf einer ganzheitlichen Portfoliosicht, d.h. zum Beispiel unter Berücksichtigung von Kreditnehmerkorrelationen, bestimmt werden können. Neben Korrelationsannahmen können in modernen Kreditportfoliomodellen zudem Diversifikationseffekte – anders als beispielsweise bei analytischen Berechnungen – dargestellt und quantifiziert werden.
Durch den Einsatz von Kreditportfoliomodellen wird auf diese Weise eine Kenntnis sowohl über die Einzelkomponenten des Portfolios als auch über das Zusammenwirken der verschiedenen Portfolio-Komponenten gewonnen, die im Reporting dargestellt wird. Hier können unter anderem die Risiken auf verschiedenen Ebenen institutsspezifisch aggregiert werden, sodass eine Übersicht der aktuellen Kreditrisikosituation der Bank geschaffen wird, welche durch zusätzliche Analyse, wie zum Beispiel der Simulation von Stressszenarien, erweitert werden kann.
Neben der Risikomessung und dem Reporting der Ergebnisse der Risikomessung dienen Kreditportfoliomodelle der Unterstützung in der operativen Risikosteuerung. Hierbei können Steuerungsimplikationen, wie zum Beispiel die Limitierung von Einzelgeschäften sowohl in Folge von berechneten Risikokennzahlen als auch resultierend aus gemessenen Konzentrationen, berücksichtigt werden. Die Modelle bilden so eine Basis zur Ableitung von Maßnahmen in einer proaktiven Risikosteuerung. Zudem können die ermittelten Ergebnisse direkt in das Pricing möglicher Neugeschäfte mit einfließen.
Nach aufsichtsrechtlichen und ökonomischen Anforderungen hat bei der Entwicklung und Implementierung eines institutseigenen Kreditportfoliomodells vor allem das Modellverständnis stark an Relevanz gewonnen. Übergreifend über die Modellfunktionalitäten muss sichergestellt werden, dass die Methodik für das Institut keine „Black Box“ darstellt und dass auch die damit einhergehende Modellvalidierung nicht vernachlässigt wird (vgl. auch Inhalt zu „Analyse eingesetzter Verfahren“ in MaRisk AT 4.1 Tz. 8). Es wird seitens der Aufsicht zudem eine Modell-Transparenz nicht nur der Funktionsweisen der Modelle selbst, sondern zusätzlich auch der genutzten Eingangsparameter wie PDs und LGDs, sowie der Vorgehensweisen zur Ermittlung anderer Eingangsdaten wie beispielsweise modellspezifischer Korrelationen (in Asset-Value-Modellen zum Beispiel sogenannter Assetkorrelationen) gefordert.
Das Ziel bei der Konzeptionierung eines institutseigenen Kreditportfoliomodells besteht im Wesentlichen darin, die bestehenden Anforderungen sowohl mittels Standardfunktionalitäten als auch durch notwendige institutsspezifische Modellerweiterungen abzudecken, dabei aber eine hohe Modelltransparenz und damit einhergehend ein tiefes Modellverständnis zu gewährleisten. Dieser Spagat stellt die zentrale Herausforderung dar, anhand eines (jederzeit erweiterbaren) Minimums an Modellkomponenten alle das Institut betreffenden Anforderungen bezüglich der Erfassung wesentlicher Kreditrisiken vollständig abzudecken.
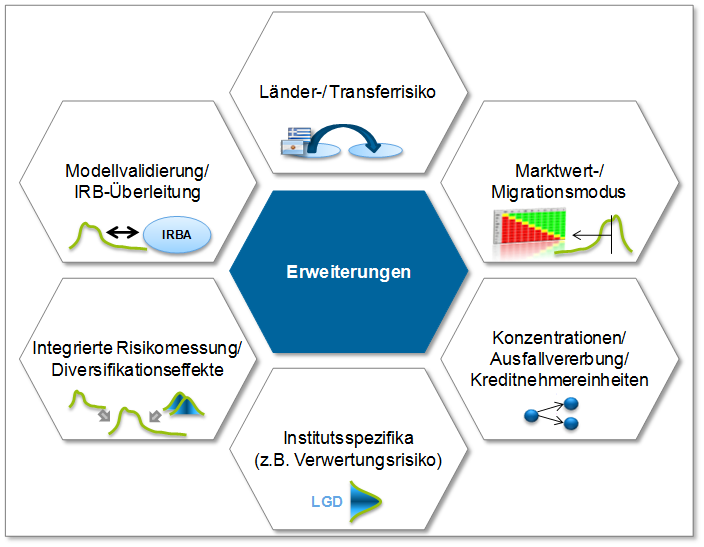
Neben den ursprünglichen Aufgaben von Kreditportfoliomodellen, klassische Adressrisiken zu messen und mit Hilfe von Risikokennzahlen wie zum Beispiel dem Value-at-Risk oder dem Expected Shortfall zu quantifizieren und abzubilden, um so die Anforderungen bezüglich Risikomessung, Reporting und Risikosteuerung zu erfüllen und dabei die Modell-Transparenz zu gewährleisten, ergeben sich je nach Art und Größe des betreffenden Instituts mögliche unterschiedliche Erweiterungen von Kreditportfoliomodellen (vergleiche Abbildung 2).
In den regulatorischen Vorgaben wird die Messung wesentlicher Risiken gefordert (vgl. MaRisk AT 2.2 Tz. 1). Im Falle von Kreditportfoliomodellen sind dazu nicht nur standardmäßig Adressausfallrisiken, sondern auch weitere relevante und insbesondere institutsspezifische (Kredit-) Risiken zu berücksichtigen. Hierbei handelt es sich beispielsweise um Länder- und Transferrisiken, die in der Regulatorik explizit genannt werden (vgl. MaRisk BTO 1.2).
Neben den klassischen Adressausfallrisiken, basierend auf direkten Ausfällen der Gegenpartei, sind – sofern relevant – auch die Migrationsrisiken, d.h. aus Ratingmigrationen bzw. Bonitätsänderungen resultierende Marktwertrisiken, vom Institut zu erfassen und zu quantifizieren (vgl. BaFin Leitplankenpapier: „Aufsichtliche Beurteilung bankinterner Risikotragfähigkeitskonzepte“ – Tz. 91). Auch die Messung der Konzentrationsrisiken innerhalb der institutsspezifisch wesentlichen Risikoarten wird direkt durch die Aufsicht gefordert (vgl. MaRisk AT 2.2 Tz. 1). Zu diesem Zweck kann in einem Kreditportfoliomodell zum Beispiel durch eine „einseitige Ausfallvererbung“ eine flexible Vorgabe von Ausfallzusammenhängen simuliert und der klassische Umgang mit Kreditnehmer-Einheiten erweitert werden. Zudem kann die Hinzunahme von Konzentrationsmaßen wie dem Gini-Koeffizient oder dem Herfindahl-Hirschman-Index (HHI) eine mögliche Erweiterung eines standardmäßigen Kreditportfoliomodells sein, um so weitere Auskunft über mögliche Klumpenrisiken zu erhalten (vgl. Vorschlag für Konzentrationsmaße in SREP Leitlinien Tz. 151).
Zur Messung wesentlicher Risiken sind auch institutsspezifische Besonderheiten und für das Institut wesentliche weitere Risikoarten in Kreditportfoliomodellen zu berücksichtigen. Als solche spezifische Risikoarten können zum Beispiel Verwertungsrisiken für ausgefallene Geschäfte oder Restwertrisiken als Spezifikation im Leasinggeschäft angeführt werden. Bei Berücksichtigung mehrerer unterschiedlicher Risikoarten in einem Kreditportfoliomodell ist sicherzustellen, dass eine integrierte Risikomessung, d.h. ein integrierter Ausweis von Adressenausfall-, Migrations- und beispielsweise Sicherheiten-Verwertungs- oder Ländertransferrisiko stattfindet und Diversifikationseffekte (vgl. MaRisk AT 4.1 Tz. 6) identifiziert werden können.
Neben der Beachtung und Integration der dargestellten weiteren (Kredit-) Risikoarten kann ein Kreditportfoliomodell ebenfalls über die Hinzunahme weiterer Modellvalidierungskomponenten erweitert werden. Diese Überprüfung bzw. Validierung könnte eine sukzessive Überleitung der im Modell ermittelten Risikowerte auf den regulatorischen Kapitalbedarf gemäß IRB-Ansatz und damit die Erklärbarkeit einzelner Risikoeffekte beinhalten, um so eine höhere Akzeptanz des Kreditportfoliomodells im Abgleich mit aufsichtsrechtlichen Werten zu erzielen. Vor dem Hintergrund der dargestellten (möglichen) Erweiterungen der Funktionalitäten eines Kreditportfoliomodells um unterschiedliche Komponenten stellt sich die Frage, wie zudem die auf den ersten Blick dazu im Kontrast stehende, aufsichtsrechtlich geforderte Modell-Transparenz eingehalten und damit die zunächst widersprüchlich erscheinende Anforderung aus Komplexität und spezifischem Verständnis erfüllt werden kann.
„Toolbox“ Kreditportfoliomodell – Modularer Lösungsansatz in der zeb-Lösung Credit
Um die dargestellten Standardfunktionalitäten bereitzustellen, dabei den ergänzenden Anforderungen an Krediportfoliomodelle gerecht zu werden und gleichzeitig eine möglichst hohe Modell-Transparenz sicherzustellen, ist ein Ansatz in Form eines modularen Funktionsbaukastens empfehlenswert. Hierbei werden die Kreditportfoliomodell-Standardfunktionalitäten anhand eines simulationsbasierten Asset-Value-Modells bereitgestellt. Dieser Modelltyp eignet sich zum einen aufgrund seiner hohen Flexibilität und vielfältigen Parametrisierbarkeit, zum anderen jedoch auch wegen seiner Nähe zur regulatorisch verwendeten IRB-Formel, die auf dem Asset-Value-Modell-Ansatz beruht. Einstmals vorherrschende Nachteile simulationsbasierter Modelle (wie zum Beispiel hoher Rechenaufwand bzw. aufwändige Simulationen) sind aufgrund von steigenden Rechenleistungen und Fortschritten im „parallel computing“ auch für große Portfolios, wie Retailportfolios, in den Hintergrund gerückt, sodass die Vorteile im Vergleich zu analytischen Modellen überwiegen.
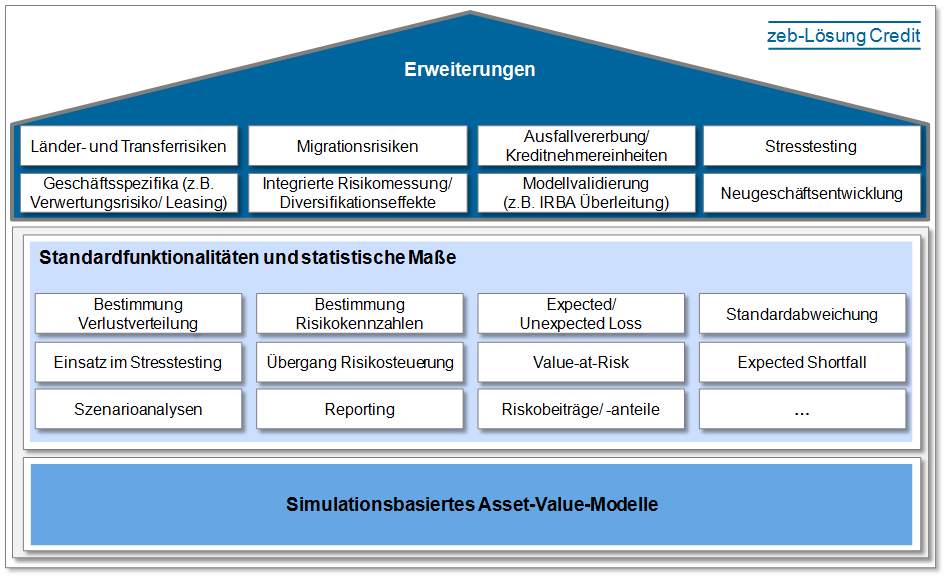
zeb bietet mit seinem Kreditportfoliomodell „zeb.control.risk – Credit“, kurz Credit, ein so implementiertes Asset-Value-Modell mit Standardfunktionalitäten und statistischen Maßen an, welches durch flexible modulare Bausteine zur Abdeckung der angesprochenen Erweiterungen und zusätzlichen Anforderungen institutsspezifisch und daher individuell ergänzt und erweitert werden kann (siehe Abbildung 3).
Die technische Umsetzung von Credit ist – einem modularen Ansatz folgend – weniger als ein zeb Risikomodell zu verstehen, denn mehr als eine Box von Bausteinen, die es jedem Institut ermöglichen sollen, gerade diejenigen Risikoaspekte zu quantifizieren, die in Anlehnung an ICAAP bzw. MaRisk Vorgaben als wesentlich identifiziert werden. Vorherrschende Institutsspezifika, d.h. die Struktur, Art und Größe der typischen Kreditportfolios des Instituts, können beachtet werden, sodass ein angemessenes Verhältnis von Aufwand und Implementierung des Kreditportfoliomodells zu Nutzen und Erkenntnisgewinn besteht und somit die Einhaltung des Proportionalitätsgedanken garantiert ist.
Credit stellt dabei eine webbasierte, flexible Lösung eines Kreditportfoliomodells dar. Gewünschte Anpassungen des Modells können vom Institut selber direkt in der Credit-Oberfläche vorgenommen werden, ohne dass eine Quellcode-Programmierung vonnöten ist. Testrechnungen und Szenarioanalysen mit Testportfolios und veränderten Einstellungen können daher anhand einfacher Anpassungen durch den Anwender leicht durchgeführt werden. Dadurch ist eine größtmögliche Modell-Flexibilität gewährleistet und die vorgegebenen Anforderungen an Kreditportfoliomodelle werden erfüllt.
Fazit und Blick in die Zukunft
In Folge der gestiegenen Anforderungen an Kreditportfoliomodelle und vor dem Hintergrund der dargestellten institutsspezifischen Modellanpassung und Modellparametrisierung hat sich gezeigt, dass simulationsbasierte Asset-Value-Modelle mit modularen Bausteinen zum einen die Standardvorgaben an Kreditportfoliomodelle abdecken, zum anderen aber auch in Anbetracht ihrer Parametrisierbarkeit eine ideale Lösung für die dargestellten Problematiken darstellen. zeb bietet mit dem simulationsbasierten Kreditportfoliomodell Credit eine Lösung an, die durch einen vereinfachten Ausbau im Falle von Anpassungsbedarf, sei es institutsspezifisch oder regulatorisch getrieben, im Laufe der Zeit so weiterentwickelt werden kann, dass eine größtmögliche Flexibilität gegeben ist und dabei stets die geforderte Modell-Transparenz eingehalten wird. Eventuelle Nachteile eines solchen simulationsbasierten Asset-Value-Modells wie zum Beispiel Credit gegenüber analytischen Methoden, aufgrund von hohen Rechenzeiten und aufwändigen Kalkulationen, sind dabei bereits – und werden in Zukunft noch weiter – dank stark steigender Rechenleistungen in den Hintergrund gerückt, so dass eine zeitgemäße und zukunftsweisende flexible Lösung geboten wird.