Daten statt Bauchgefühl – Bestimmung von Peergroups im europäischen Finanzsektor

Warum ist die traditionelle, intuitive Definition von Peergroups oft unzureichend?

In der Praxis des Wettbewerbsvergleichs erleben wir häufig, dass Peergroups recht willkürlich definiert werden bzw. wurden – oft basierend auf einer Marktexpertise oder einem Bauchgefühl. Die definierten Peergroups bleiben oftmals auch über Jahre hinweg konstant, ohne dass Geschäftsmodellveränderungen objektiv analysiert werden. Wir haben uns gefragt: Sind die jeweils definierten Peers tatsächlich (immer noch) der analysierenden Bank strukturell ähnlich? Oder vergleichen wir manchmal Äpfel mit Birnen?

Wir wollten herausfinden, welche Banken wirklich ähnliche Geschäftsmodelle haben – also objektiv und reproduzierbar. Es ging uns nicht darum, die aktuelle Praxis zu kritisieren. Vielmehr wollten wir eine datengetriebene Methodik entwickeln, um weitere Erkenntnispunkte bei der Definition von Peergroups zu erzeugen. Am Ende müssen Anwendende und Ersteller:innen von Peergroup-Vergleichen entscheiden, wer mit wem verglichen werden soll. Unsere Methode mag weitere Einblicke liefern.

Mit objektivierbar anlegbaren Maßnahmen können wir gegebenenfalls ein zentrales Problem der ausschließlich erfahrungsbasierten Peergroup-Analyse umgehen. Menschen neigen dazu, sich allzu stark an ihrer eigenen Erfahrung zu orientieren. Damit mögen sie wesentliche Entwicklungen übersehen oder Fehleinschätzungen der Vergangenheit nicht erkennen. Zudem stellen unterschiedliche Stakeholder auch unterschiedliche Peergroups zusammen: Nicht immer sind die Peergroups des Managements deckungsgleich mit denen der Vergleichsinstitute, die Equity-Analyst:innen heranziehen.

Unser Ziel war es, eine Hilfestellung zu geben, um eine Art objektiver, datengetriebener Peer-Landschaft des europäischen Bankensektors ableiten zu können. Wir wollten ganz konkret einen Weg finden, der hilft, Peers datengetrieben zu identifizieren – und damit losgelöst von jeglichen „hidden agendas“. Wir wollten zeigen, dass man Strukturen auf einer quantitativen Basis identifizieren kann – ohne erfahrungsbasierte Vorannahmen. Das Ziel war, robuste Cluster zu bilden, die echte strukturelle Nähe widerspiegeln: Wer ist wem tatsächlich ähnlich, wenn man Finanzkennzahlen und Bilanzstrukturen berücksichtigt?

Das ist in unserer Tätigkeit als Unternehmensberater bei zeb eine sehr häufige Fragestellung, und bisher waren unsere Aussagen dazu eher heuristisch. Eine Idee für die Zukunft wäre, die Methodik in einem für all unsere Kolleg:innen und Kund:innen nutzerfreundlichen Tool bereitzustellen, das sie bei ihrer Arbeit und der Peergroup-Auswahl unterstützt.

Datengrundlage: Welche KPIs werden herangezogen?

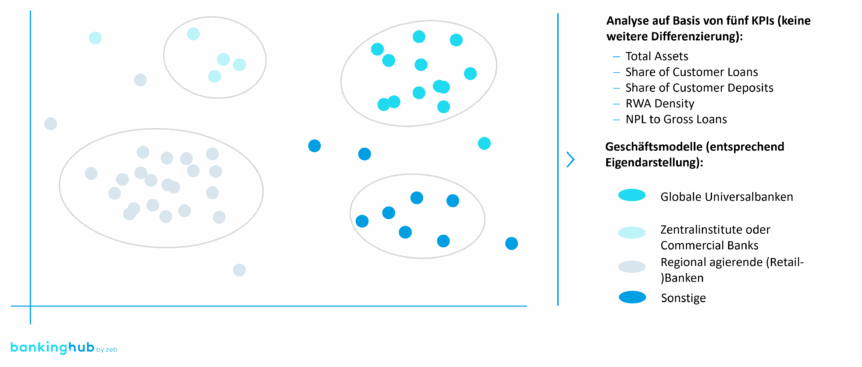
Bei datengetriebenen Analysen ist offensichtlich die Datenauswahl ausschlaggebend. Wir haben uns entschieden, in dieser ersten Analyse die 50 führenden europäischen Banken zu betrachten, und fünf zentrale KPIs ausgewählt, die die Struktur und das Geschäftsmodell einer Bank gut abbilden: die Bilanzsumme, den Anteil von Kundenkrediten und Einlagen, die RWA-Dichte und das Verhältnis von Non-Performing Loans zu Gross Loans. Diese Kennzahlen sind breit genug, um unterschiedliche Bankentypen zu erfassen, aber spezifisch genug, um Strukturen differenzieren zu können.

Wir haben uns bewusst auf eine kleine Anzahl von KPIs fokussiert. Wir wollten Abstand von zu vielen Dimensionen nehmen, um nicht ein „Rauschen“ durch überlappende oder redundante Kennzahlen zu erzeugen.

Diese fünf KPIs verdeutlichen die wesentlichen Unterschiede: Bilanzgröße, Kundenorientierung, Risikoexposition und Stabilität. Damit lässt sich bereits erstaunlich viel erklären. Rein technisch geht die Methodik für 15 Kennzahlen aber im Übrigen gleichermaßen gut. Und selbstverständlich funktioniert die Methodik auch bei kleineren, regional operierenden Instituten.

Wäre es nicht spannend, wenn man etwa beim Benchmarking von Regionalbanken in Deutschland weniger auf regionale Vergleichbarkeit als vielmehr auf strukturelle Vergleichbarkeit abstellen würde?

Methode: Wie wird die strukturelle Ähnlichkeit von Banken mathematisch dargestellt?

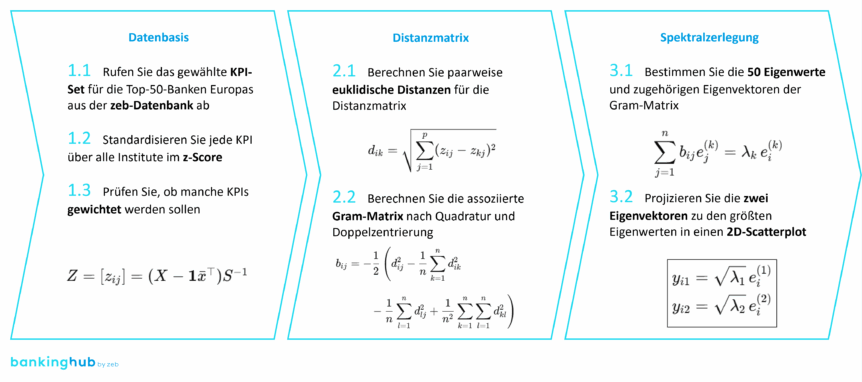
In der von uns entwickelten Methode zur Ableitung von Peergroups verwenden wir das Konzept der euklidischen Distanzmessung. Für nichtmathematische Leser:innen mag das komplex klingen. Tatsächlich ist die Methode aber nicht neu und wurde bereits vor langer Zeit eingeführt: Man stelle sich jede Bank als einen Punkt in einem mehrdimensionalen Raum vor – jede Achse entspricht einer Kennzahl.

Zwei Banken, die in allen Dimensionen ähnliche Werte haben, liegen nah beieinander; zwei mit stark unterschiedlichen Werten liegen weit auseinander. Diese Entfernung im Raum misst man mit der euklidischen Distanz – also mit der „Luftlinie“ zwischen den Punkten. Kleine Distanzen bedeuten hohe strukturelle Ähnlichkeit, große Distanzen zeigen Divergenzen. Im Folgenden findet sich eine anonymisierte grafische Darstellung dieser Divergenzen.

Abbildung 1: Bankencluster auf Basis der gewählten Methode (anonymisiert und vereinfacht)

Aufmerksame Leser:innen erkennen, dass die Ergebnisse in einem zweidimensionalen Clusterplot dargestellt werden. Es bleibt damit die Frage offen, wie man von einem hochdimensionalen Raum zu dieser Ebenendarstellung kommen kann. Auch hier verwenden wir eine bereits seit Langem eingesetzte Methode.

Die Rückführung auf zwei Ebenen geschieht über eine sogenannte metrische multidimensionale Skalierung (MDS). Sie nimmt die Distanzmatrix aus dem n-dimensionalen Raum (hier n = 5) und projiziert sie so in zwei Dimensionen, dass die Abstände zwischen den Punkten möglichst gut erhalten bleiben. Mathematisch basiert das auf einer Eigenwertzerlegung der transformierten Gramschen Matrix – also etwas linearer Algebra. So kann man die komplexen Zusammenhänge visuell greifbar machen. Das ist in der Anschauung einfacher, als es klingt: Man stelle sich etwa vor, man kennt nur die Entfernungen zwischen den zehn größten deutschen Städten – aber nicht deren tatsächliche geografische Koordinaten. Über diese Entfernungen lässt sich dennoch die relative Lage aller Städte zueinander eindeutig rekonstruieren, bis auf die Drehung und Spiegelung der gesamten Karte. Das ist genau die Idee hinter der MDS für die Banken, denn die Dimension des Raums, in welchem euklidische Distanzen definiert werden, ist dabei vollkommen egal.

Abbildung 2: Methodik der Peer- und Clusteranalyse

Wir glauben, dass in dieser Anwendung linearer Algebra für Fortgeschrittene die Besonderheit unserer Methode liegt. In der leicht zu berechnenden 1.-Person-Perspektive fragt man: Wer sind die nächsten Nachbarn im Raum? Man braucht keine komplette Karte, keine höhere Mathematik – die Distanzen reichen, um zu erfassen, mit wem man sich am meisten ähnelt.

In der neuartigen 3.-Person-Perspektive hingegen sehen wir das gesamte Feld von oben – sozusagen in der Vogelperspektive –, obwohl das unmittelbar angesichts des hochdimensionalen Raums nicht umsetzbar wäre. Wir betrachten die Lage aller Banken relativ zueinander, erkennen Cluster, Übergänge und Abstände. Beide Perspektiven ergänzen sich: Die erste ist praktisch für konkrete Vergleiche, die zweite analytisch hilfreich für das große Ganze.

Welche Grenzen muss man bei der Interpretation der Ergebnisse beachten?

Wir haben die Methodik auf den Datenbestand angewandt und mit typischen Peer-Analysen verglichen. Die Ergebnisse aus der Mathematik und die typischen Peergroup-Cluster der Praktiker:innen haben sich in diesem Set-up zu großen Teilen gegenseitig bestätigt. Das hat uns einerseits überrascht. Natürlich erwartet man, dass die Geschäftsmodelle von den Praktiker:innen richtig bewertet werden. Aber die Klarheit, mit der sich Cluster formen, war beeindruckend. Das spricht für die Robustheit des Ansatzes. Zudem haben wir innerhalb der Cluster die konkrete Anordnung der jeweiligen Institute in der Ebene, die die Interpretation deutlich vereinfacht.

Selbstverständlich sind die Grenzen der gewählten Methodik immer zu beachten. Zwei Hauptpunkte sollen hier genannt werden: Erstens misst die euklidische Distanz rein lineare Zusammenhänge. Nichtlineare Unterschiede, etwa durch qualitative Geschäftsmodellfaktoren, werden nicht vollständig erfasst. Zweitens hängt das Ergebnis stark von der Skalierung und Gewichtung der Kennzahlen ab – hier braucht man also methodische Sorgfalt. Die Methode ersetzt kein Expertenurteil, sie ergänzt es quantitativ.

Welchen Mehrwert bietet die datengetriebene Methode Analyst:innen, Banken und Aufsichtsbehörden?

Mit unserer Methode kann Sicherheit geschaffen werden, in der Peergroup-Analyse nichts zu übersehen und nicht mehr, wie so häufig, dem „Groupthink“ anheimzufallen. Wenn bereits gewählte Peergroups durch die Mathematik bestätigt werden, dann umso besser. Konkret sehen wir folgenden „Value-add“ unserer Methode:

• Analyst:innen und Investor:innen bietet sie eine objektive Basis für die Definition von Peergroups.
• Banken liefert sie wertvolle Hinweise zur Positionierung: Mit wem bin ich tatsächlich vergleichbar?
• Der Aufsicht und Zentralbanken kann sie helfen, strukturelle Cluster und systemische Risiken zu erkennen – jenseits von Länderkategorien.

Für Rückfragen, Anmerkungen und intensive Diskussionen zu dieser Methode steht das Autorenteam jederzeit zur Verfügung!