Ausgangssituation
Anforderungen und Erwartungen an Kreditportfoliomodelle sind in den letzten Jahren aufgrund erhöhter regulatorischer Vorgaben und veränderten Marktbedingungen, die insbesondere zur Notwendigkeit erhöhter Modellflexibilität und ‑individualität führen, gestiegen. Gleichzeitig sind auch die technischen Möglichkeiten bzgl. der Rechenleistung, u. a. aufgrund von Fortschritten im „parallel computing“, deutlich gewachsen. Aus diesen Gründen rücken Asset-Value-basierte Simulationsmodelle – für die zwar eine hohe Rechenleistung benötigt wird, die aber ein deutlich höheres Maß an Flexibilität in der Modellierung bieten – zur Quantifizierung von Kreditportfoliorisiken immer mehr in den Fokus der Banken.
Zur Messung der (unerwarteten) Verluste haben sich dabei die quantilbasierten Risikomaße Value at Risk (VaR) sowie Expected Shortfall (ES) etabliert. Der 99%-Quantilwert einer Verlustverteilung gibt beispielsweise die Portfolioverlusthöhe an, die mit 99%iger Wahrscheinlichkeit innerhalb einer Periode nicht überschritten wird. Der unerwartete Verlust wird dann als Differenz aus Quantilwert und erwartetem Verlust quantifiziert. Unabhängig davon, ob der VaR als Quantilwert oder unerwarteter Verlust definiert wird[1], wird im VaR keine Aussage zu Verlusten jenseits des entsprechenden Quantils getroffen. Dies erfolgt im Expected Shortfall (ES), da dieser als der gewichtete Durchschnitt über alle Verlusthöhen oberhalb des Quantilwerts definiert wird. Der ES beschreibt also das Tailrisiko und gibt Auskunft über die erwartete Höhe extremer Portfolioverluste. Abbildung 1 bietet hierzu einen Überblick.
Die Quantifizierung erwarteter und unerwarteter Verluste ist in der Regel aber nicht nur auf Portfolioebene interessant, sondern unter Risikosteuerungsgesichtspunkten insbesondere auf Einzelkreditnehmerebene von Relevanz. Dabei stellt sich die Frage, welchen Beitrag ein Kreditgeschäft oder ein Kreditnehmer zum Gesamtrisiko in Form des VaR oder ES auf Portfolioebene beiträgt. Da es sich beim ES-Maß im Gegensatz zum VaR um ein kohärentes Risikomaß handelt, werden in modernen Kreditportfoliomodellen auch die Risikobeiträge von Einzelgeschäften oder ‑kreditnehmern zum Portfolio-VaR anhand der jeweiligen Beiträge zum Expected Shortfall – dem marginalen Expected Shortfall (mES) – verteilt. Auf diese Weise ist auch die (Sub-)Additivität der VaR-Beiträge sichergestellt.
Werden die individuellen Risikobeiträge dann zu Risikobeurteilungs- und Risikosteuerungszwecken – z. B. dem verursachungsgerechten Pricing von Konzentrationen – eingesetzt, so ist es erforderlich, dass die berechneten Beiträge zwischen verschiedenen, gleich parametrisierten Berechnungsläufen möglichst wenig variieren, also stabil sind. Ebenso sollten die Risikobeiträge zweier ähnlicher Kreditnehmer mit vergleichbaren Risikopositionen ähnlich groß sein. Die Frage nach einer hinreichend hohen Stabilität ist spezifisch für Simulationsmodelle und liegt darin begründet, dass sich für diese Art von Modellen die Verteilung der Portfolioverluste nicht analytisch bestimmen lässt, sondern numerisch approximiert wird. Das grundsätzliche Vorgehen dieser als Monte-Carlo-Simulation bezeichneten Methode besteht darin, potenzielle Realisationen der Portfolioverlustverteilung zu ziehen. Diese Ziehung zufälliger Verluste wird viele Male wiederholt, sodass am Ende eine große Anzahl an potenziellen Portfolioverlusten vorliegt, deren Häufigkeitsverteilung gegen die Verteilung der Portfolioverluste konvergiert. Entsprechend ist bei Simulationsmodellen die geforderte Stabilität in der Regel nur über die Durchführung einer sehr hohen Anzahl an Ziehungen zu erreichen.
Bei Verwendung des 99%- bzw. 99,9%-Quantils können beispielsweise dann nur die 1 % bzw. 0,1 % der Ziehungen mit dem höchsten Portfolioverlust zur Berechnung des ES herangezogen werden. Aus diesem Grund wird schnell klar, dass bereits für den ES, insbesondere aber für die Risikobeiträge einzelner Kreditnehmer eine deutlich höhere Anzahl an durchzuführenden Ziehungen benötigt wird, damit stabile Ergebnisse gewährleistet werden können. Dies steht im Konflikt mit der Tatsache, dass Ziehungen Zeit kosten und Kreditportfoliomodelle in der Praxis nicht beliebig lang laufen können, wenn die Ergebnisse dem Risikomanagement zeitnah zur Verfügung stehen sollen.
Eine Lösung dieses Konflikts zwischen ausreichender Stabilität der simulierten unerwarteten Verluste – auch auf Einzelkreditnehmerebene – und einer akzeptablen Laufzeit liefert speziell bei komplexen Kreditportfolios die Varianzreduktionstechnik des Importance Sampling.
Importance Sampling führt zur Erhöhung der Stabilität im Tailbereich
Die Grundidee des Importance Sampling liegt darin – wie der Name bereits suggeriert – die Gewichtung der Wahrscheinlichkeit bei der Simulation, also der Ziehung der Portfolioverluste zu verschieben. Während bei der klassischen Monte-Carlo-Simulation jede Ziehung als gleich wahrscheinlich angenommen wird und die Streuung um den Erwartungswert nur aufgrund der Zufallseinflüsse entsteht, wird beim Importance Sampling die Wahrscheinlichkeit für die Ziehung besonders hoher Portfolioverluste, also im Tailbereich, signifikant erhöht. Die Gewichtung wird im Optimum so gewählt, dass die Wahrscheinlichkeit, über dem jeweils „echten“ Portfolio-VaR zu liegen, von 1 % bzw. 0,1 % auf ca. 50 % steigt.[2] Auf Basis dieser neuen Wahrscheinlichkeitsgewichtung der Portfolioverluste wird anschließend – wie im klassischen Ansatz – eine gewisse Anzahl an Portfolioverlusten gezogen und deren Verteilung analysiert. Da nun eine deutlich höhere Anzahl an Ziehungen in dem für die VaR- und ES-Berechnung besonders interessanten Bereich der hohen Portfolioverluste liegt, wird die Stabilität der Ergebnisse in diesem Bereich durch das Importance Sampling deutlich erhöht. Tabelle 1 bietet hierzu einen beispielhaften Überblick.
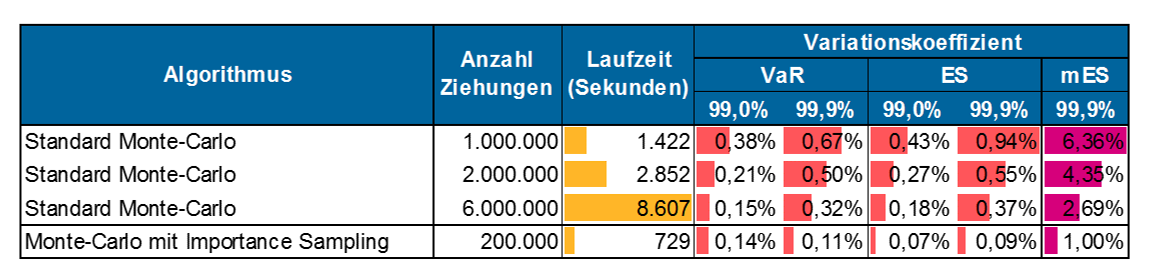 Tabelle 1: Vergleich der Stabilität der Simulationsergebnisse für gewöhnliche Monte-Carlo Simulation und Importance Sampling
Tabelle 1: Vergleich der Stabilität der Simulationsergebnisse für gewöhnliche Monte-Carlo Simulation und Importance SamplingDie Stabilität wird dabei durch den Variationskoeffizienten quantifiziert.[3] Neben VaR und ES ist dieser für den marginalen ES abgetragen, der per Definition die höchste Volatilität aufweist, für das Pricing von Kreditrisiken, insbesondere von Konzentrationen, jedoch zunehmend an Bedeutung gewinnt und entsprechend stabil gegenüber zufälligen Einflüssen sein muss. Es wird deutlich, dass Importance Sampling zu einer erheblichen Erhöhung der Stabilität der Risikomaße speziell im „Problembereich“ des marginalen ES führt. Selbst wenn man die Anzahl der Ziehungen im Beispiel von 6 Mio. auf 200.000 reduziert, sind die sich ergebenden Risikomaße bei Verwendung des Importance Sampling stabiler als im klassischen Monte-Carlo-Ansatz. Die Laufzeit kann bei gleichbleibender Stabilität auf etwa 5–10 % des klassischen Monte-Carlo-Ansatzes reduziert werden.
Bei einem Blick auf die Laufzeiten im Vergleich zur Anzahl der Ziehungen in Tabelle 1 wird allerdings deutlich, dass die einzelnen Ziehungen bei Verwendung des klassischen Importance-Sampling-Algorithmus deutlich länger dauern. Dies ist dem Umstand geschuldet, dass pro Simulationsziehung durch die zweistufige Gewichtung sowie das (Zurück‑)Transformieren der Wahrscheinlichkeiten deutlich mehr Schritte gerechnet werden müssen. Der klassische, optimale Importance-Sampling-Algorithmus ist so konstruiert, dass er im Sinne der Anzahl an Ziehungen und der Minimalität der Variation optimal ist. Dabei steht nicht die Laufzeit der einzelnen Ziehungen im Fokus.
Vor dem Hintergrund der Laufzeitreduktion kann es sinnvoll sein, auf bestimmte, insbesondere rechenintensive Teile des optimalen Importance-Sampling-Algorithmus zu verzichten. Die berechneten Risikomaße weisen dann zwar nicht mehr die theoretisch optimale Stabilität (bei gleicherbleibender Anzahl an Ziehungen) auf. Im Praxiseinsatz kann dies allerdings über die Reduktion der Kalkulationslaufzeit je Ziehung überkompensiert werden.
Dieser Überkompensationseffekt wird weiter verstärkt, wenn das Kreditportfoliomodell vom Standardansatz eines Asset-Value-basierten Kreditportfoliomodells abweicht. Davon ist in der Praxis auszugehen, da ein großer Vorteil Asset-Value-basierter Kreditportfoliomodelle eben darin liegt, dass sie sich flexibel um kundenindividuelle Funktionalitäten erweitern lassen.
Herausforderungen bei Verwendung von Importance Sampling in flexiblen Modellen mit Zusatzfunktionalitäten
Individuell erweiterbare Kreditportfoliomodelle, wie z. B. das Asset-Value-basierte Model Credit 3.00[4] von zeb, bieten eine Vielzahl an Erweiterungen, welche sich kundenindividuell anpassen lassen. Ein Beispiel ist die mögliche Integration der Modellierung potenzieller Länderausfälle. Dies führt dazu, dass jedes Kreditengagement aufgrund von zwei Ereignissen ausfallen kann. Zum einen kann ein Länderausfall auf gewisse Weise zum Ausfall der gesamten Kreditengagements innerhalb dieses Landes führen. Zum anderen kann ein Kreditengagement aufgrund individueller Umstände ausfallen. Credit 3.00 beispielsweise erlaubt dabei sowohl eine separate als auch eine integrierte Betrachtung des Risikos, welches sich aus Länderausfällen (Länderrisikomodus LRM) und individuellen Ausfällen (Ausfallrisikomodus ARM) ergibt. Der integrierte Fall wird im Gesamtrisikomodus (GRM) dargestellt.
In Tabelle 2 sind die resultierenden Ergebnisse für die Stabilität der Simulation aufgeführt, wenn die Möglichkeit von Länderausfällen integriert wird. Dabei sind die Ergebnisse neben denen für den klassischen Monte-Carlo-Ansatz einmal für den theoretisch optimalen Importance-Sampling-Algorithmus („Monte-Carlo mit Importance Sampling“) sowie für eine individuell angepasste Umsetzung des Importance-Sampling-Algorithmus in Credit 3.00 enthalten.
 Tabelle 2: Vergleich der Stabilität der Simulationsergebnisse für gewöhnliche Monte-Carlo Simulation und Credit 3.00 mit Importance Sampling für Länder- (LRM), Ausfall- (ARM) und Gesamtrisikomodus (GRM).
Tabelle 2: Vergleich der Stabilität der Simulationsergebnisse für gewöhnliche Monte-Carlo Simulation und Credit 3.00 mit Importance Sampling für Länder- (LRM), Ausfall- (ARM) und Gesamtrisikomodus (GRM).Es wird deutlich, dass der theoretisch optimale Importance-Sampling-Algorithmus im klassischen Ausfallmodus (ARM) im Vergleich zur Standard-Monte-Carlo-Simulation weiterhin deutlich bessere Werte liefert. Im Ländermodus sowie der Kombination der beiden Ausfallmodi, also dem GRM, sind die Ergebnisse bzgl. des Variationskoeffizienten aber bei Weitem nicht mehr zufriedenstellend und liegen sogar hinter dem klassischen Monte-Carlo-Ansatz.
So sinnvoll die Integration der Länderausfallkomponente bei der Risikoquantifizierung sein kann, ergibt sich aber vor dem Hintergrund von Importance Sampling das Problem, dass ein Kreditengagement, auch wenn im GRM sowohl der länderinduzierte als auch der individuelle Ausfall simultan eintritt, nur einmal ausfällt. Dieser „Überlappung“ von Ereignissen gilt es beim Wechsel des Wahrscheinlichkeitsmaßes und dessen Rückrechnung entsprechend Rechnung zu tragen und erfordert eine Anpassung des Importance-Sampling-Algorithmus.
Hohe Laufzeitreduktion bei Verwendung von individuell angepassten Algorithmen
Die für Credit 3.00 angepasste Version des Algorithmus hingegen liefert – wie in Tabelle 2 zu sehen ist – weiterhin einen deutlichen Stabilitätszuwachs gegenüber dem klassischen Monte-Carlo-Ansatz.
In Credit 3.00 werden die notwendigen Anpassungen des klassischen Importance-Sampling-Algorithmus deshalb abhängig von den kundenindividuell integrierten Funktionalitäten vorgenommen, sodass in verschiedenen Ausgestaltungsmöglichkeiten des Modells mithilfe von Importance Sampling hohe Aufwandseinsparungen realisiert werden können. Im Regelfall kann die Laufzeit damit um mindestens 90 % gegenüber einem klassischen Monte-Carlo-Ansatz verringert werden.
Neben der Möglichkeit der Integration von potenziellen Länderausfällen bieten moderne Kreditportfoliomodelle weitere Erweiterungsmöglichkeiten wie beispielsweise
- die Modellierung von stochastischen, ggf. abhängigen Verlustquoten (LGD) bei Ausfall eines Kreditengagements,
- die Modellierung von Ratingmigrationen von Kreditengagements (zusätzlich zu Ausfällen, Marktwertmodus) sowie
- die Modellierung von Kreditengagements mit unterjähriger Restlaufzeit.
Alle spezifischen Modellerweiterungen müssen bei der Implementierung eines Importance-Sampling-Algorithmus berücksichtigt werden und erfordern eine individuelle Anpassung des Ansatzes. Dies macht eine „standardmäßige“ Integration der Importance-Sampling-Idee schwierig.
Fazit
Steigende regulatorische und ökonomische Anforderungen erfordern immer flexiblere und individuelle Lösungen, um bankspezifische Kreditrisiken möglichst gut quantifizieren zu können. Die dazu besonders geeigneten simulationsbasierten Kreditportfoliomodelle erfordern jedoch eine hohe Anzahl an durchzuführenden Simulationsziehungen, welche in der Regel mit einer hohen Laufzeit einhergehen.
Mithilfe eines auf spezifische Modellkonfigurationen angepassten Importance-Sampling-Ansatzes lässt sich die Stabilität gegenüber der klassischen Monte-Carlo-Simulation bei gleicher oder sogar reduzierter Laufzeit stark erhöhen. Dazu sind jedoch von der Konfiguration abhängige Parametrisierungen und Anpassungen des Importance-Sampling-Algorithmus erforderlich. Im zeb Kreditportfoliomodell Credit 3.00 wird deshalb die Standardidee des Importance Sampling so angepasst, dass trotz der Verwendung weiterer Modellfunktionalitäten eine möglichst hohe Einsparung der Laufzeit erreicht wird und gleichzeitig stabile Ergebnisse geliefert werden.





Eine Antwort auf “Simulationsbasierte Risikomodellierung – Fokussierung auf das Wesentliche”
Marc Räkers
Weiterführende Informationen zu „zeb.control.risk – Credit“ unter:
https://control.zeb.eu/services/banking/risk#credit